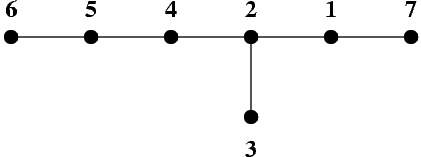
A graph is a pair (V, E), where V is a finite set of elements called vertices of the graph, and E is a subset of the set of all unordered pairs of distinct vertices. The elements of the set E are called edges of the graph. If for each pair of distinct vertices u, v there exists exactly one sequence of distinct vertices w₀, w₁, ..., w_k, such that w₀ = u, w_k = v and the pairs {w_i, w_i + 1} are in E, for i = 0, ..., k - 1, then the graph is called a tree. We say that the distance between the vertices u and v in the tree is k.

It is known that a tree of n vertices has exactly n - 1 edges. A tree T whose vertices are numbered from 1 to n can be unambiguously described by giving the number of its vertices n, and an appropriate sequence of n - 1 pairs of positive integers describing its edges.

Any permutation of vertices - i.e. a sequence in which each vertex appears exactly once - is called a traversing order of a tree. If the distance of each two consecutive vertices in some order of the tree T is at most c, then we say that it is a traversing order of the tree with step c.

It is known that for each tree its traversing order with step 3 can be found.

Example

This tree can be traversed with step 3 by visiting its vertices in the following order: 7 2 3 5 6 4 1.

Task

• reads a description of a tree from the text file DRZ.IN,
• finds an arbitrary traversing order of that tree with step 3,
• writes that order in the text file DRZ.OUT.

Input

• In the first line of the file DRZ.IN there is a positive integer n, not greater than 5000 - it is the number of vertices of the tree.
• In each of the following n - 1 lines there is one pair of positive integers separated by a single space and representing one edge of the tree.

Output

Example

7
1 2
2 3
2 4
4 5
5 6
1 7

7
2
3
5
6
4
1