Box of Mirrors
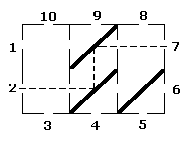
BOI 2001 Day 1 Problem 3Mathematician Andris likes different puzzles and one of his favorites is covered box of mirrors. If we look at the horizontal cross-section of such a box, we can see that its basement contains n*m square cells (n rows, and m columns). In each cell there can be placed mirror which is oriented diagonally from lower left corner to upper right corner. Both sides of the mirror reflect light. At the box edges opposite to each cell row or column there is a gap through which you can light a beam into box or the beam can come out of the box. Through each gap you can light the beam in only one direction--perpendicular to the edge containing the gap. Therefore, beam reflecting from mirror changes its direction by 90 degrees. When the beam goes through empty cells, its direction doesn't change. Gaps are numbered consecutively from 1 to 2*(n+m), around the box, counter-clockwise, starting from the gap on the left side of the upper left cell and going downwards. Since arrangement of mirrors in the box is not visible, the only way to determine it is by lighting beams in some gaps and watching where light comes out.
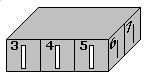 TaskWrite program that:
If there are several possible solutions, your program should output anyone of them. InputFirst line of input file box.in contains two positive integers: n (the number of cells rows, 1<=n<=100) and m (the number of cells columns, 1<=m<=100) separated by a single space. Each of the following 2*(n+m) lines contains one positive integer. The number in the i+1-th line denotes the number of gap from which light comes out if it is lightened into gap number i.OutputYour program should write to the output file box.out n lines, each of them containing m integers separated by single spaces. The j-th number in the i-th line should be 1, if there is a mirror in the cell in the i-th row and j-th column of the box, or it should be 0 if the cell is empty.Sample Input2 3 9 7 10 8 6 5 2 4 1 3 Sample Output0 1 0 0 1 1
 SubmitStatistics
SubmitStatistics |

